Table of Contents

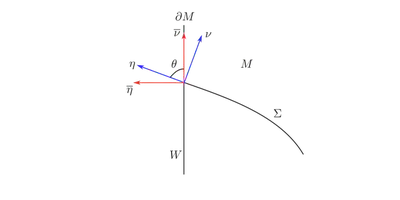
We set the following notations. Suppose $(M^{n+1},\partial M)$ is the ambient manifold we’re interested in. We say $\Sigma$ is a capillary minimal surface with contact ange $\theta$ if $\Sigma$ is a minimal surface with boundary $\partial \Sigma$ and it has contact angle $\theta$ with $\partial M$ along $\partial \Sigma$.

First Variation Formula

Suppose $\partial \Sigma$ bounds a region $W$ in $\partial M$ with outer unit normal $\overline{\nu}$, then $\Sigma$ is a capillary minimal surface if and only if it is a critical point of the following functional, $$ \mathcal{A}(\Sigma)=\left|\Sigma\right|-\cos \theta \left|W\right|. $$ This can be seen from the following argument.

Let $X$ be the variational vector field. Then, $$ \left.\frac{d}{dt}\right|_{t=0}\mathcal{A}(\Sigma_t)=\int_{\Sigma}\mathrm{div}_\Sigma XdA-\cos\theta\int_{ M}\mathrm{div}_MXdA. $$ Now if we suppose $X|_{\partial M} \in \mathfrak{X}(\partial M)$, then $$ \int_{ M} \mathrm{div}_MXdA= \int_{ \partial \Sigma} X\cdot \overline{\nu} ds. $$

So $$ \left. \frac{d}{dt}\right|_{t=0}\mathcal{A}(\Sigma_t)={} \int_{ \Sigma} X \cdot \nu H dA+\int_{ \partial \Sigma} (X \cdot \eta-\cos \theta X\cdot \overline{\nu})ds. $$ Suppose $\eta$ makes angle $\varphi$ with $T(\partial M)$, (i.e., $\eta=\cos \varphi \overline{\nu}+\sin \varphi \overline{\eta}$), then $X\cdot \eta = \cos \theta X \cdot \overline{\nu}$. Hence, $\Sigma$ is a critical point if and only if $H\equiv 0$ and $\varphi=\theta$ along $\partial \Sigma$.

Fix a unit vector $v \in \partial H=\mathbb{R}^{n-1}$. Choose two constant vectors $\nu_1=-\cos \theta \overline{\eta} + \sin \theta v, \nu_2=-\cos \theta \overline{\eta}-\sin \theta v$.

Then we replace $\varphi$ by $\varphi \sqrt{(1-\nu \cdot \nu_1)(1-\nu \cdot \nu_2)}$ in the stability inequality.

Stability inequality, choose $A(X,Y)= \left< \nabla_{X}Y, \nu \right>$. $$\int_{ \Sigma} \left|\nabla \varphi\right|^2-\left|A\right|^2\varphi^2+ \int_{ \partial \Sigma} \cot \theta A(\eta,\eta) \varphi^2\ge 0.$$

Preliminary identities. $$\begin{aligned} \nu={} & -\cos \theta \overline{\eta}+\sin \theta \overline{\nu} \ \eta={} & \sin \theta \overline{\eta}+\cos \theta \overline{\nu} \ 1 -\nu \cdot \nu_1={}& 1-\cos ^2 \theta-\sin ^2\theta \overline{\nu}\cdot v = \sin ^2\theta(1-\overline{\nu}\cdot v) \ 1 -\nu\cdot\nu_2={}& 1-\cos ^2\theta+\sin ^2\theta \overline{\nu}\cdot v=\sin ^2\theta(1+\overline{\nu}\cdot v)\ \frac{\partial }{\partial \eta}(1-\nu \cdot \nu_1)={}& - \frac{\partial }{\partial \eta}\nu \cdot \nu_1 = A(\eta,\eta)\eta \cdot \nu_1=A(\eta,\eta)(-\sin \theta\cos \theta +\sin \theta\cos \theta \overline{\nu}\cdot v) \ ={}& -\sin \theta\cos \theta A(\eta,\eta)(1-\overline{\nu}\cdot v) \ \frac{\partial }{\partial \eta}(1-\nu\cdot\nu_2)={}& -\sin \theta\cos \theta A(\eta,\eta)(1+\overline{\nu}\cdot v) \end{aligned}$$

Now we may insert $\varphi \sqrt{(1-\nu\cdot\nu_1)(1-\nu\cdot\nu_2)}$ in stability inequality. (Let $w = \sqrt{(1-\nu\cdot\nu_1)(1-\nu\cdot\nu_2)}$) $$\begin{aligned} {} & \int_{ \Sigma} \left|A\right|^2(1-\nu\cdot\nu_1)(1-\nu\cdot\nu_2) \varphi^2\ \le{} & \int_{ \Sigma} w^2 \left|\nabla \varphi\right|^2+\varphi^2\left|\nabla w\right|^2+ \frac{1}{2}\int_{ \Sigma} \nabla \varphi^2\cdot \nabla w^2 \ {}&+\int_{ \partial \Sigma} A(\eta,\eta) \cot \theta \varphi^2 \sin ^4 \theta(1-\overline{\nu}\cdot v)(1+\overline{\nu}\cdot v)\ ={} & \int_{ \Sigma} w^2 \left|\nabla \varphi\right|^2+\varphi^2\left|\nabla w\right|^2- \frac{1}{2}\int_{ \Sigma} \varphi^2 \Delta w^2+ \frac{1}{2}\int_{ \partial \Sigma} \varphi^2 \frac{\partial }{\partial \eta}w^2 \ {}&+\int_{ \partial \Sigma} A(\eta,\eta)\varphi^2 \sin^3 \theta \cos \theta(1-\overline{\nu}\cdot v)(1+\overline{\nu}\cdot v) \end{aligned}$$

We compute $\frac{\partial }{\partial \eta}w^2$. $$\begin{aligned} \frac{\partial }{\partial \eta}w^2={} & (1-\nu\cdot\nu_2)\frac{\partial }{\partial \eta}(1-\nu\cdot\nu_1)+(1-\nu\cdot\nu_1)\frac{\partial }{\partial \eta}(1-\nu\cdot\nu_2)\ ={} & \sin ^2 \theta (1+\overline{\nu}\cdot v)\times - \sin \theta \cos \theta A(\eta,\eta)(1-\overline{\nu}\cdot v)\ {}& +\sin ^2\theta (1-\overline{\nu}\cdot v) \times -\sin \theta\cos \theta A(\eta,\eta)(1+\overline{\nu}\cdot v) \ = {}& -2\sin ^3\theta \cos \theta A(\eta,\eta)(1-\overline{\nu}\cdot v)(1+\overline{\nu} \cdot v) \end{aligned}$$

Hence, the boundary term can be cancelled out.

Let’s focus on $\Delta w^2.$ $$\begin{aligned} \Delta w^2={} & -(1-\nu \cdot \nu_2)\Delta(\nu \cdot \nu_1)-(1-\nu \cdot \nu_1)\Delta(\nu \cdot \nu_2)+2(\nabla \nu \cdot \nu_1)\cdot(\nabla \nu\cdot\nu_2) \ ={} & (1-\nu \cdot\nu_2) \left|A\right|^2(\nu \cdot \nu_1)+(1-\nu\cdot\nu_1)\left|A\right|^2(\nu\cdot\nu_2)+(\nabla \nu \cdot \nu_1)\cdot(\nabla \nu\cdot\nu_2)\ ={}& \left|A\right|^2(\nu\cdot\nu_1+\nu\cdot\nu_2-2 \left( \nu\cdot\nu_1 \right)\cdot (\nu\cdot\nu_2))+(\nabla \nu \cdot \nu_1)\cdot(\nabla \nu\cdot\nu_2) \end{aligned}$$

$$\begin{aligned} LHS={} & \int_{ \Sigma} \left|A\right|^2(1-2\cos ^2 \theta + (\nu\cdot\nu_1)(\nu\cdot \nu_2))\varphi^2 \ \int_{ \Sigma} \left|A\right|^2(1-\cos ^2\theta)\varphi^2\le{} & \int_{ \Sigma} w^2 \left|\nabla \varphi\right|^2+\varphi^2 \left|\nabla w\right|^2-{(\nabla \nu \cdot \nu_1)\cdot(\nabla \nu\cdot\nu_2)}\varphi^2. \end{aligned}$$

$\nu\cdot\nu_1+\nu\cdot\nu_2=2\cos ^2 \theta$

Now we note $$\begin{aligned} \left|\nabla w\right|^2 -(\nabla \nu \cdot \nu_1)\cdot (\nabla \nu\cdot\nu_2)={} & \frac{\left|(1-\nu\cdot\nu_1)(\nabla \nu\cdot\nu_2)-(1-\nu\cdot \nu_2)(\nabla \nu\cdot\nu_1)\right|^2}{4w^2} \end{aligned}$$

Some useful formulas $$\left|\nabla \nu \cdot p\right|^2= \sum_{i =1}^{n}h_{1i}^2(\left|p\right|^2-(p\cdot \nu)^2).$$

Note that $$\begin{aligned} \mathrm{I}:={} & \left|\nabla \nu \cdot \left( \left( 1-\nu\cdot\nu_1 \right)\nu_2-(1-\nu \cdot \nu_2)\nu_1 \right)\right|^2 \ ={} & |\nabla \nu \cdot ( (1+\cos \theta \overline{\eta}\cdot\nu-\sin \theta v \cdot\nu)(-\cos \theta \overline{\eta}-\sin \theta v)\ &-(1+\cos \theta \overline{\eta}\cdot \nu-\sin \theta v\cdot \nu)(-\cos \theta\overline{\eta}+\sin \theta v) )|^2\ ={}& 4\sin ^2 \theta\left|\nabla \nu \cdot (-(1+\cos \theta \overline{\eta}\cdot \nu)v+\cos \theta v \cdot\nu \overline{\eta})\right|^2 \end{aligned}$$

Note that $$(-(1+\cos \theta \overline{\eta}\cdot\nu)v+ \cos \theta v \cdot \nu\overline{\eta})\cdot \nu=- v \cdot \nu.$$

Hence $$\begin{aligned} \mathrm{I}={} & 4\sin ^2\theta \sum_{ }^{}h_{1i}^2((1+\cos \theta \eta\cdot \nu)^2+\cos ^2 \theta \left( v \cdot \nu \right)^2- (v\cdot\nu)^2)\ ={} & 4\sin ^2\theta \sum_{ }^{}h_{1i}^2 \left( (1+\cos \theta \eta\cdot\nu)^2-\sin ^2\theta (v\cdot\nu)^2 \right) \end{aligned}$$

On the other hand, we know $$w^2 = (1+\cos \theta \overline{\eta} \cdot \nu-\sin \theta a\cdot \nu)(1+\cos \theta\overline{\eta}\cdot\nu+\sin \theta v\cdot\nu)$$

So we get $$\mathrm{I}=4 \sin ^2\theta \sum h_{1i}^2 w^2.$$

In summary, we get $$\int_{ \Sigma} \sin ^2\theta \left|A\right|^2\le \int_{ \Sigma} w^2 \left|\nabla \varphi\right|^2+\int_{ \Sigma} \sin ^2\theta \sum h_{1i}^2.$$

Using Schoen-Simon’s inequality, we have the following inequality $$\int_{ \Sigma} \left|A\right|^2\varphi^2\le C_\theta \int_{ \Sigma} (1-\nu\cdot\nu_1)(1-\nu\cdot\nu_2)\left|\nabla \varphi\right|^2.$$

First variation formula

Suppose $\partial \Sigma$ bounds a region $W$ in $\partial M$ with outer unit normal $\overline{\nu}$, then $\Sigma$ is a capillary minimal surface if and only if it is a critical point of the following functional. $$\mathcal{A}(\Sigma)=\left|\Sigma\right|-\cos \theta \left|M\right|.$$

::: proof Proof. Let $X$ be the variational vector field, then $$\begin{aligned} \left. \frac{d}{dt}\right|{t=0} & \mathcal{A}(\Sigma_t)= \int{ \Sigma} \mathrm{div}\Sigma X dA - \cos \theta\int{ M} \mathrm{div}_M X dA.

\end{aligned}$$

Now if we suppose $X|{\partial M} \in \mathfrak{X}(\partial M)$, then $$\int{ M} \mathrm{div}MXdA= \int{ \partial \Sigma} X\cdot \overline{\nu} ds$$

So $$\begin{aligned} \left. \frac{d}{dt}\right|{t=0}\mathcal{A}(\Sigma_t)={} & \int{ \Sigma} X \cdot \nu H dA+\int_{ \partial \Sigma} (X \cdot \eta-\cos \theta X\cdot \overline{\nu})ds \end{aligned}$$

Suppose $\eta$ makes angle $\varphi$ with $T(\partial M)$, (i.e. $\eta=\cos \varphi \overline{\nu}+\sin \varphi \overline{\eta}$), then $X\cdot \eta = \cos \theta X \cdot \overline{\nu}$.

Hence, $\Sigma$ is a critical point if and only if $H\equiv 0$ and $\varphi=\theta$ along $\partial \Sigma$. ◻ :::

Relation of capillary minimal surfaces and minimal triple junction surfaces. Considering $\theta=\frac{2\pi}{3}$, we know $\mathcal{A}(\Sigma)=\left|\Sigma\right|+\frac{1}{2}\left|W\right|$. Let $\Sigma’$ be the reflection of $\Sigma$ with respect to $\partial M$ (e.g. suppose $M$ is a standard half space), then $(\Sigma,\Sigma’, W)$ will be a minimal triple junction surfaces and the energy function for these surfaces should be $\mathcal{A}=\left|\Sigma\right|+\left|\Sigma’\right|+\left|M\right|$.

Second variation formula

$$\int_{ \Sigma} \left|\nabla \phi\right|^2-\left|A\right|^2\phi^2+ \int_{ \partial \Sigma} \left( \frac{A _{\partial M}(\overline{\nu},\overline{\nu})}{\sin \theta}+ \cot \theta A(\eta,\eta) \right)\phi^2.$$

We choose the special vector fields as $X = \left< X, \nu \right>\nu +\left< X, \eta \right> \eta= \phi \nu + \cot \theta \phi \eta=\frac{1}{\sin \theta} \phi \overline{\nu}$.

We still write $\phi= X\cdot \nu$. First term. $$\begin{aligned} \left. \frac{d}{dt}\right|{t=0}\int{ \Sigma}X\cdot \nu_t H_t dA_t= {} & \int_{ \Sigma} X\cdot \nu H’ dA + \int_{ \Sigma} H \left. \frac{d}{dt}\right|{t=0}(X\cdot \nu_t)dA_t \end{aligned}$$ We can use $H’ = \Delta{\Sigma}\phi+\left|A\right|^2\phi$. So the interior part is given by this term.

For the boundary term, we need to compute $$\begin{aligned} \left. \frac{d}{dt}\right|{t=0} \int{ \partial \Sigma} (X\cdot \eta_t - \cos \theta X \cdot \overline{\nu}t)ds_t ={} & \int{ \partial \Sigma} \left< X, \eta-\cos \theta \overline{\nu} \right>’ ds. \end{aligned}$$

So we need to compute $\eta’, \overline{\nu}’$.

First, let’s compute $\nu’$. Let $\left{ e_i \right}$ be the orthonormal basis of $T_p \Sigma$. Then $$\begin{aligned} \left< \nu’, e_i \right> ={} & -\left< \nu, e_i’ \right> = -\left< \nu ,D _{e_i}X \right> =-\left< \nu, D {e_i}(\phi \nu + \left< X, e_j \right> e_j) \right> \ ={} & -e_i(\phi)-\left< X, e_j \right> h{ij} \end{aligned}$$

Hence $\nu’ = - \nabla_{\Sigma}\phi-A(X^\top ,e_i )e_i$.

Now $\left< \eta’, \nu \right> =- \left< \eta,\nu’ \right> =\frac{\partial }{\partial \eta}\psi + A(X^T, \eta)$.

We also have $$\begin{aligned} \left< \eta’, \tau_i \right> ={}& -\left< \eta, \tau_i’ \right> = -\left< \eta, D _{\tau_i}X \right> = \phi A(\eta, \tau_i)+\cot \theta \tau_i(\phi)\ \end{aligned}$$

So $$\eta’ = \left( \frac{\partial \phi}{\partial \eta}+A(X^T, \eta) \right)\nu + \phi A(\eta,\tau_i)\tau_i+\cot \theta \nabla_{\partial \Sigma} \phi.$$

Hence $$\begin{aligned} \left< X, \eta’-\cos \theta \overline{\nu}’ \right> ={} & \frac{\phi}{\sin \theta}\left< \overline{\nu}, \eta’-\cos \theta \overline{\nu}’ \right> =\frac{\phi}{\sin \theta} \left< \overline{\nu}, \eta’ \right> \ ={} & \phi \left( \frac{\partial \phi}{\partial \eta} + \cot \theta\phi A(\eta,\eta)\right) \end{aligned}$$

Moreover, $$\left< X’, \eta - \cos \theta \overline{\nu} \right> = \left< \nabla_{X}X, \sin \theta \overline{\eta} \right> = \frac{\phi^2}{\sin\theta} A _{\partial M}(\overline{\nu},\overline{\nu}).$$

Generalized Bernstein Theorem

We know the curvature estimate for stable capillary surfaces will be related to the generalized Bernstein Theorem in half space $H = \left{ x_1\ge 0 \right}$.

Here, we will prove the generalized Bernstein Theorem for capillary surfaces in $H^3$.

::: theorem Theorem 1. If $(\Sigma,\partial \Sigma) \hookrightarrow (H^3, \partial H)$ is a stable capillary minimal surface with quadratic area growth condition. Then $\Sigma$ is flat. :::

The stability inequality becomes $$\int_{ \Sigma} \left|A\right|^2 \phi ^2dA\le \int_{ \Sigma} \left|\nabla \phi\right|^2dA+ \int_{ \partial \Sigma} \cot \theta A(\eta,\eta)\phi^2ds.$$

Dealing with boundary term

Let’s choose $w = 1+\left< \nu, \overline{\eta} \right>\cos \theta$. Replace $\phi$ by $\phi w$ in stability inequality. We note $$\begin{aligned} \int_{ \Sigma} \left|\nabla (\phi w)\right|^2={} & \int_{ \Sigma} w^2 \left|\nabla \phi\right|^2+ \phi^2 \left|\nabla w\right|^2+\frac{1}{2}\int_{ \Sigma} \left< \nabla \phi^2, \nabla w^2 \right> \ ={} & \int_{ \Sigma} w^2 \left|\nabla \phi\right|^2-\phi^2 w \Delta w + \int_{ \partial \Sigma} \phi^2 w \frac{\partial w}{\partial \eta}. \end{aligned}$$

Note that we have $$\Delta w = \cos \theta \Delta \left< \nu ,\overline{\eta} \right> = -\cos \theta \left< h_{ij}e_j, \overline{\eta}\right> _i= -\cos \theta\left|A\right|^2 \left< \nu, \overline{\eta} \right>$$ and $$\frac{\partial w}{\partial \eta}=\cos \theta \left< \frac{\partial \nu}{\partial \eta}, \overline{\eta} \right> =-\cos \theta \sin \theta A(\eta,\eta)=-\cot \theta A(\eta,\eta)w.$$

Here, we’ve used $w=1-\cos ^2\theta=\sin ^2\theta$ along $\Gamma$.

So in summary, we will get $$\int_{ \Sigma} \left|A\right|^2 w\phi^2 dA\le \int_{ \Sigma} \left|\nabla \phi\right|^2w^2dA.$$

So we will get the following inequality $$\int_{ \Sigma} \left|A\right|^2\phi^2dA\le C_\theta \int_{ \Sigma} \left|\nabla \phi\right|^2dA$$

Choose special test functions (logarithmic cutoff function)

We will control the curvature $\left|A\right|$ in the half ball $B_1 \cap H$.

Choose $\phi$ as follows $$\phi= \begin{cases} 1, & \left|x\right|\le 1, \ 1- \frac{\log \left|x\right|}{n}, & 1\le \left|x\right|\le e^n,\ 0, & \left|x\right|\ge e^n. \end{cases}$$

Then, we can find $$\begin{aligned} \int_{ \Sigma \cap B_1} \left|A\right|^2dA\le {} & C \int_{ \Sigma \cap B {e^n}\backslash B_1} \frac{1}{\left|x\right|^2 n^2} dA\le C \sum{i =1}^{n} \int_{ \Sigma \cap B {e^i}\backslash B{e^{i-1}}}\frac{1}{e^{2i-2} n^2}dA \ \le {} & C \sum_{i =1}^{n} \frac{C e^2}{n^2}= \frac{C}{n}. \end{aligned}$$ Now we may choose $n\rightarrow 0$ to get $\left|A\right|\equiv 0$ in $B_1$. The unique continuation of minimal surfaces tells us $\Sigma$ is flat.