Scalar curvature comparison of rotationally symmetric sets

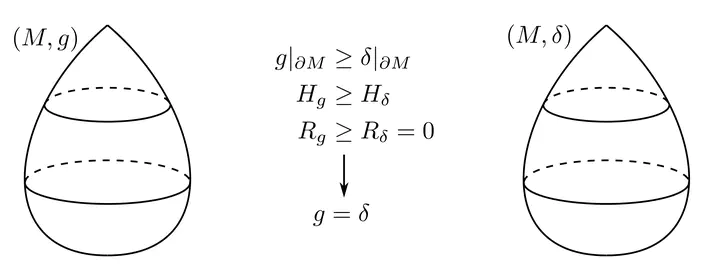
Abstract

Suppose $M$ is a rotationally symmetric convex set in $\mathbb{R}^3$ with two different metric $g$ and $\delta$ (the standard Euclidean metric). Then for some special $M$ with the condition $g_{\partial M}\ge \delta_{\partial M},H_g\ge H_\delta, R_g\ge R_\delta$, then we can show that $g=\delta$.